Download the notebook here! Interactive online version: binder

Instrumental variable estimators of causal effects

Overview

  • Causal effect estimation with a binary IV

  • Traditional IV estimators

  • Instrumental variable estimators in the presence of individual-level heterogeneity

  • Conclusions

Causal effect estimation with a binary IV

We consider the standard relationship

\begin{align*} Y = \alpha + \delta D +\epsilon, \end{align*}

where \(\delta\) is the true causal effect that (for now) is assumed to be constant.

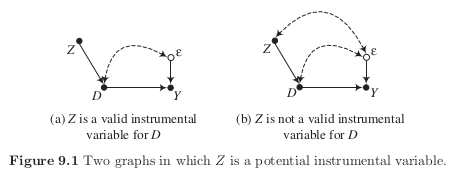
2c8f4fce00ce46d0911ef5193289e5c2

  • No conditioning estimator would effectively estimate the causal effect of \(D\) on \(Y\) because no observed variable satisfy the back-door criterion.

  • If perfect stratification cannot be be enacted with the available data, one possible solution is to find an exogenous source of variation that determines \(Y\) only by way of the causal variable \(D\). The causal effect is then estimated by measuring how much \(Y\) varies with the proportion of the total variation in \(D\) that is attributable to the exogenous variation.

\begin{align*} E[Y] = E[\alpha + \delta D + \epsilon] = \alpha + \delta E[D] + E[\epsilon] \end{align*}

We can rewrite this as a difference equation in \(Z\):

\begin{align*} E[Y \mid Z = 1] - E[Y \mid Z = 0] = \delta (E[D \mid Z = 1] - E[D \mid Z = 0]) + (E[\epsilon \mid Z = 1] - E[\epsilon \mid Z = 0]) \end{align*}

Then we divide both sides by \(E[D \mid Z = 1] - E[D \mid Z = 0]\).

\begin{align*} \frac{E[Y \mid Z = 1] - E[Y \mid Z = 0]}{E[D \mid Z = 1] - E[D \mid Z = 0]} = \frac{\delta (E[D \mid Z = 1] - E[D \mid Z = 0]) + (E[\epsilon \mid Z = 1] - E[\epsilon \mid Z = 0])}{E[D \mid Z = 1] - E[D \mid Z = 0]} \end{align*}

If Figure 9.1 (a) is an accurate description of the causal structure, then \(E[\epsilon \mid Z = 1] = E[\epsilon \mid Z = 0] = 0\).

\begin{align*} \frac{E[Y \mid Z = 1] - E[Y \mid Z = 0]}{E[D \mid Z = 1] - E[D \mid Z = 0]} = \delta \end{align*}
\begin{align*} \hat{\delta}_{IV, WALD} = \frac{E[Y \mid Z = 1] - E[Y \mid Z = 0]}{E[D \mid Z = 1] - E[D \mid Z = 0]} \end{align*}

  • The assumption that \(\delta\) is an invariant structural effect is crucial for this result.

Demonstration dataset

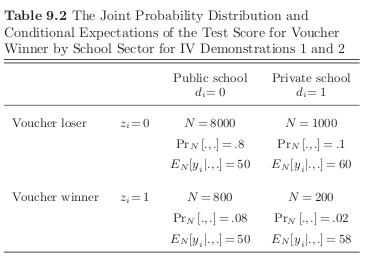
We wish to determine whether private high school outperform public high schools as measured by \(9^{th}\) grade achievement tests. There exists a school voucher program in the city that covers tuition in case one attends private school. However, there are budgetary limits and so the vouchers are available only to 10% of students and allocated by a lottery.

01a563320d7b41b88478b9e3303da330

  • Winning the lottery increases private school attendance.

[2]:

def get_sample_iv_demonstration():
    """Simulates sample.

    Simulates a sample of 10,000 individuals for the IV demonstration
    based on the information provided in our textbook.

    Notes:

        The school administration distributed 1,000 vouchers for
        private school attendance in order to shift students
        from public into private school. The goals is to increase
        educational achievement.

    Args:
        None

    Returns:
        A pandas Dataframe with the observable characteristics (Y, D, Z)
        for all individuals.

        Y: standardized test for 9th graders
        D: private school attendance
        Z: voucher available

    """
    # We first initialize an empty Dataframe with 10,000 rowns and three
    # columns.
    columns = ["Y", "D", "Z"]
    index = pd.Index(range(10000), name="Identifier")
    df = pd.DataFrame(columns=columns, index=index)

    # We sample the exact number of individuals following the description
    # in Table 9.2.
    for i in range(10000):
        if i < 8000:
            y, d, z = np.random.normal(50), 0, 0
        elif i < 9000:
            y, d, z = np.random.normal(60), 1, 0
        elif i < 9800:
            y, d, z = np.random.normal(50), 0, 1
        else:
            # The lower mean for the observed outcome does indicate
            # that those drawn into treatment due to the instrument
            # only do have smaller gains compared to those that
            # take the treatment regardless.
            y, d, z = np.random.normal(58), 1, 1

        df.loc[i, :] = [y, d, z]

    # We shuffle all rows so we do not have the different subsamples
    # grouped together.
    df = df.sample(frac=1).reset_index(drop=True)

    # We set the types of our columns for prettier formatting later.
    df = df.astype(np.float)
    df = df.astype({"D": np.int, "Z": np.int})

    return df

Let’s have a look at the structure of the data.

[3]:

df = get_sample_iv_demonstration()
df.head()

[3]:
Y D Z
0 48.606920 0 0
1 50.240003 0 0
2 49.377337 0 0
3 60.885880 1 0
4 50.160785 0 0

How about the conditional distribution of observed outcomes?

[4]:

df.groupby(["D", "Z"])["Y"].mean()

[4]:

D  Z
0  0    50.009760
   1    49.962199
1  0    60.034692
   1    58.072959
Name: Y, dtype: float64

We can always run an OLS regression first to get a rough sense of the data.

[5]:

rslt = smf.ols(formula="Y ~ D", data=df).fit()
rslt.summary()

[5]:
OLS Regression Results
Dep. Variable: Y R-squared: 0.904
Model: OLS Adj. R-squared: 0.904
Method: Least Squares F-statistic: 9.374e+04
Date: Wed, 16 Jun 2021 Prob (F-statistic): 0.00
Time: 08:40:03 Log-Likelihood: -14482.
No. Observations: 10000 AIC: 2.897e+04
Df Residuals: 9998 BIC: 2.898e+04
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 50.0054 0.011 4555.317 0.000 49.984 50.027
D 9.7023 0.032 306.173 0.000 9.640 9.764
Omnibus: 12.957 Durbin-Watson: 2.022
Prob(Omnibus): 0.002 Jarque-Bera (JB): 13.196
Skew: -0.074 Prob(JB): 0.00136
Kurtosis: 3.100 Cond. No. 3.13


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

However, to exploiting the structure of the dataset, we rather want to compute the IV estimate.

[6]:

def get_wald_estimate(df):
    """Calculate Wald estimate.

    Calculates the Wald estimate for the causal effect of treatment
    on an observed outcome using a binary instrument.

    Args:
        df: A pandas DataFrame

    Returns:
        A float with the estimated causal effect.

    """
    # We compute the average difference in observed outcomes.
    average_outcome = df.groupby("Z")["Y"].mean().to_dict()
    numerator = average_outcome[1] - average_outcome[0]

    # We compute the average difference in treatment uptake.
    average_treatment = df.groupby("Z")["D"].mean().to_dict()
    denominator = average_treatment[1] - average_treatment[0]

    rslt = numerator / denominator

    return rslt

So, let’s see.

[7]:

rslt = get_wald_estimate(df)
print(" Wald estimate: {:5.3f}".format(rslt))

 Wald estimate: 5.183

Traditional IV estimators

We now move beyond a binary instrument.

\begin{align*} \hat{\delta}_{IV} \equiv \frac{Cov_N(y_i, z_i)}{Cov_N(d_i, z_i)} \end{align*}

Moving towards the population-level relationships:

\begin{align*} \frac{Cov(Y, Z)}{Cov(D, Z)} & = \frac{\delta Cov(D, Z) + Cov[\epsilon, Z]}{Cov(D, Z)} \\ & = \delta \end{align*}

So, this suggests that:

\begin{align*} \frac{Cov_N(y_i, z_i)}{Cov_N(d_i, z_i)} \xrightarrow{p} \delta \end{align*}

fc84e55afd5f417eb2978ebfc33f12d8

Returning to our simulated example, we can now apply the two-stage least squares (2SLS) estimator you are familiar with.

[8]:

df["D_pred"] = smf.ols(formula="D ~ Z", data=df).fit().predict()
smf.ols(formula="Y ~ D_pred", data=df).fit().summary()

[8]:
OLS Regression Results
Dep. Variable: Y R-squared: 0.002
Model: OLS Adj. R-squared: 0.002
Method: Least Squares F-statistic: 17.39
Date: Wed, 16 Jun 2021 Prob (F-statistic): 3.07e-05
Time: 08:40:03 Log-Likelihood: -26171.
No. Observations: 10000 AIC: 5.235e+04
Df Residuals: 9998 BIC: 5.236e+04
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 50.5478 0.153 330.860 0.000 50.248 50.847
D_pred 5.1830 1.243 4.170 0.000 2.747 7.619
Omnibus: 3794.296 Durbin-Watson: 1.993
Prob(Omnibus): 0.000 Jarque-Bera (JB): 11127.197
Skew: 2.065 Prob(JB): 0.00
Kurtosis: 6.107 Cond. No. 38.0


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Given the structure of our example, both estimators are equivalent. As of now, statsmodels does not provide good support for the instrumental variables estimation. That is true for a host of methods often used by economists. Often linearmodels provides a viable alternative.

[11]:

from linearmodels import IV2SLS  # noqa: E402

df["const"] = 1
IV2SLS(df["Y"], df["const"], df["D"], df["Z"]).fit()

[11]:
IV-2SLS Estimation Summary
Dep. Variable: Y R-squared: 0.7076
Estimator: IV-2SLS Adj. R-squared: 0.7075
No. Observations: 10000 F-statistic: 77.109
Date: Wed, Jun 16 2021 P-value (F-stat) 0.0000
Time: 08:43:00 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
Parameter Std. Err. T-stat P-value Lower CI Upper CI
const 50.548 0.0748 676.20 0.0000 50.401 50.694
D 5.1830 0.5902 8.7812 0.0000 4.0261 6.3398


Endogenous: D
Instruments: Z
Robust Covariance (Heteroskedastic)
Debiased: False
id: 0x7f19084a4d60

Instrumental variable estimators in the presence of individual-level heterogeneity

\begin{align*} Y & = Y^0 + D (Y^1 - Y^0) \\ & = Y^0 + \delta D \\ & = \mu^0 + \delta D + \nu^0, \end{align*}

where \(\mu^0 \equiv E[Y^0]\) and \(\nu^0 \equiv Y^0 - E[Y^0]\). Here, \(\delta\) now has a clear interpretation.

We need to add a four-category latent variable \(C\):

\begin{align*} \text{Compliers (C = c)} & : D^{Z = 0} = 0 \,\text{and}\, D^{Z = 1} = 1 \\ \text{Defiers (C = d)} & : D^{Z = 0} = 1 \,\text{and}\, D^{Z = 1} = 0 \\ \text{Always takers (C = a)} & : D^{Z = 0} = 1 \,\text{and}\, D^{Z = 1} = 1 \\ \text{Never takers (C = n)} & : D^{Z = 0} = 0 \,\text{and}\, D^{Z = 1} = 0 \\ \end{align*}

Analogously to the definition of the observed outcome, \(Y\), the observed treatment indicator variable \(D\) can then be defined as

\begin{align*} D & = D^{Z = 0} + (D^{Z = 1} - D^{Z = 0}) Z \\ &= D^{Z = 0} + \kappa Z \end{align*}

What is the value of \(\kappa\) for the different latent groups?

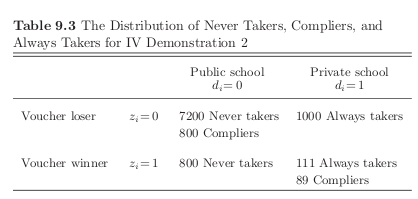
Identifying assumptions for the Local Average Treatment Effect

  • Independence, \((Y^1, Y^0, D^{Z = 1}, D^{Z = 0}) \perp \!\!\! \perp Z\)

  • Nonzero effect of instrument, \(\kappa \neq 0\) for at least some \(i\)

  • Monotonicty assumption, either \(\kappa \geq 0\) for all \(i\) or \(\kappa \leq 0\) for all \(i\)

If these assumptions are valid, then an instrument \(Z\) identifies the \(LATE\): the average treatment effect for the subset of the population whose treatment selection is induced by the treatment.

\begin{align*} \hat{\delta}_{IV,WALD} \xrightarrow{p} E [\delta \mid C = c] \end{align*}

ad458fcb322f48c0a835e64437c0cd17

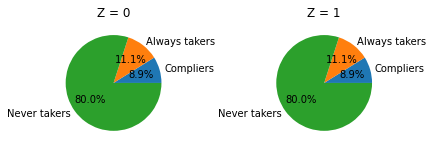
What can we learn about the different latent groups?

  • Monotonicity, there are no defiers

  • Independence, the same distribution of never takes, always takers, and compliers is present among voucher groups

\begin{align*} \frac{Pr_N [d_i = 1, z_i = 0]}{Pr_N[z_i = 0]} \xrightarrow{p} Pr[C = a] \\ \frac{Pr_N [d_i = 0, z_i = 1]}{Pr_N[z_i = 1]} \xrightarrow{p} Pr[C = n] \\ \end{align*}

We also know \(Pr[C = d] = 0\) and thus

\begin{align*} 1 - \frac{Pr_N [d_i = 1, z_i = 0]}{Pr_N[z_i = 0]} - \frac{Pr_N [d_i = 0, z_i = 1]}{Pr_N[z_i = 1]}\xrightarrow{p} Pr[C = c] \\ \end{align*}

596ba2b696cb4391b60d8a56197622a2

How can we learn about the LATE from the information analyzed so far?

\begin{align*} E[\delta \mid C = c] = E [Y^1 - Y^0 \mid C = c] \end{align*}

Let’s start with the following:

\begin{align*} E[Y \mid D = 1, Z = 1] & = \frac{Pr[C = c]}{Pr[C = c] + Pr [C=a]} E[Y^1 \mid C = c] \\ &+ \frac{Pr[C = a]}{Pr[C = c] + Pr [C=a]} E[Y^1 \mid C = a] \\ &\\ E[Y \mid D = 0, Z = 0] & = \frac{Pr[C = c]}{Pr[C = c] + Pr [C=n]} E[Y^0 \mid C = c] \\ & + \frac{Pr[C = n]}{Pr[C = c] + Pr [C=n]} E[Y^0 \mid C = n] \end{align*}

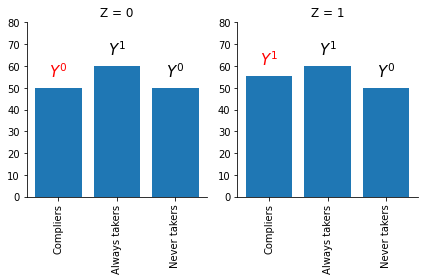
Note that we can consistent estimates for \(E[Y^0 \mid C = n]\) and \(E[Y^1 \mid C = a]\) are provided in the table directly.

Now lets tie this back to the Wald estimator:

\begin{align*} \hat{\delta}_{IV, WALD} = \frac{E[Y \mid Z = 1] - E[Y \mid Z = 0]}{E[D \mid Z = 1] - E[D \mid Z = 0]} \end{align*}
[12]:

get_shares_latent_groups()
../../_images/lectures_instrumental-variable_notebook_26_0.png 
[13]:

get_outcome_latent_groups()
../../_images/lectures_instrumental-variable_notebook_27_0.png

Criticism

  • instrument-dependent parameter

  • limited policy-relevance

Discussion

We revisit and discuss the discussion of the LATE’s usefulness.

27f196094945443c806fd3881ae58a5e

b09594ee9eb94d479708911a161edfde

Table of contents

  • Introduction

  • Background and Data

    • National Random Selection

    • Social Security Earnings Data

  • The Effect of Draft Eligibility and Earnings

  • The Effect of Military Service on Earnings

    • Estimates Using Draft Eligibility

    • Efficient Instrumental Variables Estimates

  • Military Service of Labor Market Experience

  • Caveats

    • Treatment Effect Heterogeneity

    • The Absence of Covariates

    • Earnings-Modifying Draft Avoidance Behavior

  • Conclusions

4f61ae6f7e224b6f8376b860c26c409d

5d840a037617431b885ff304454aa671

Table of contents

  • Introduction

  • Season of Birth, Compulsory Schooling, and Years of Education

    • Direct Evidence and teh Effect of Compulsory Schooling Laws

    • Why do Compulsory Schooling Laws Work?

  • Estimating the Returns to Education

    • TSLS Estimation

    • Allowing the Seasonal Pattern in Education to Vary by State of Birth

    • Estimates for Black Men

  • Other Possible Effects of Season of Birth

  • Conclusions

eae25b56bf144602b36605df6b98d806

We discuss Rosenzweig & Wolpin (2000) in more detail because it provides a small structural economic model of schooling choice that allows to interpret the instrumental variable estimates of Angrist (1990) and Angrist & Krueger (1991).

\begin{align*}\begin{array}{ll} a &\text{age} \\ y_a & \text{earnings at age a} \\ S & \text{level of schooling attainment} \\ X_a & \text{work experience at age $a$} \\ \mu & \text{ability} \\ a_e & \text{school entry age} \\ a_\kappa & \text{minimum age to leave school}\\ S_0 = a_\kappa - a_e & \text{minimum schooling} \\ c & \text{direct cost of education} \end{array}\end{align*}

Wages are determined as follows:

\begin{align*} \ln y_a = f(S, \mu) + g(X_a, \mu) \end{align*}

The authors assume that individuals work full-time after school and there is no uncertainty about wages. Individuals decide whether to pursue one additional year of schooling after the mandatory minimum. If they do so \(s_1\) takes value one and zero otherwise. So, the final level of schooling is \(S_1 = S_0 + s_1\). All individuals work \(A\) periods in the labor market. Spending one additional year in school does not reduce total time in the labor market. However, it results in entering the labor market one year later as schooling precludes working. Ability is the only source of heterogeneity and distributed at random in the population.

The individual’s objective is to choose their final level of schooling such as to maximize their discounted lifetime earnings under the two scenarios \((V_1, V_0)\).

\begin{align*}\begin{array}{ll} V_1(S_1 = 1 | S_0) &= -c + \sum_{a=0}^{A-1} \beta^{a + 1} y_a \\ &= -c + \sum_{a=0}^{A-1} \beta^{a + 1} \exp(f(S_0 + 1, \mu) + g(a, \mu)) \\ &= -c + \sum_{a=0}^{A-1} \beta^{a + 1} \exp(f(S_0 + 1, \mu)) \exp(g(a, \mu)) \\ &= -c + \exp(f(S_0 + 1, \mu)) \sum_{a=0}^{A-1} \beta^{a + 1} \exp(g(a, \mu)) \end{array}\end{align*}
\begin{align*} V_1(S_1 = 0 | S_0) &= \sum_{a=0}^{A-1} \beta^a y_a \\ &= \exp(f(S_0, \mu)) \sum_{a=0}^{A-1} \beta^a \exp(g(a, \mu)) \end{align*}

We now turn attention to the decision rule \(V_1 > V_0\) implies further pursuit of education.

\begin{align*}\begin{array}{ll} -c + \exp(f(S_0 + 1, \mu) \sum_{a=0}^{A-1} \beta^{a + 1} \exp(g(a, \mu)) \\ > \exp(f(S_0 + 1, \mu)) \sum_{a=0}^{A-1} \beta^a \exp(g(a, \mu) \\[20pt] -c + \exp(f(S_0 + 1, \mu) \sum_{a=0}^{A-1} \beta^{a + 1} \exp(g(a, \mu)) \\ > \underbrace{\exp(f(S_0 + 1, \mu)) \sum_{a=0}^{A-1} \beta^a \exp(g(a, \mu)}_{V_1(S_1 = 0 | S_0)} \end{array}\end{align*}

now divide by \(V_1(S_1 = 0 | S_0)\)

\begin{align*}\begin{array}{ll} \frac{\exp(f(S_0 + 1, \mu))}{\exp(f(S_0, \mu))} \beta &> 1 + \frac{c}{V_1(S_1 = 0 | S_0)} \\ &> (1 + \frac{c}{V_1(S_1 = 0 | S_0)}) (1 + r) \\ f(S_0 + 1, \mu) - f(S_0, \mu) &> r + \frac{c}{V_1(S_1 = 0 | S_0)} \end{array}\end{align*}

using \(\ln (1 + x) \approx x\) for small \(x\).

\begin{align*} s_1 = \begin{cases} 1 & \text{if}\quad f(S_0 + 1, \mu) - f(S_0, \mu) \geq r + \ln\left(\frac{c}{V_1(s_1 = 0 \mid S_0)} + 1\right) \\ 0 & \text{otherwise} \end{cases} \end{align*}

If ability increases the marginal schooling return, then there exists a unique cutoff value for ability \(\mu^*\) such that individuals with ability above the cutoff continue schooling while those below do not.

\begin{align*} \frac{\partial f(S_0 + 1, \mu) - f(S_0, \mu)}{\partial \mu} > 0 \end{align*}

Even if randomly assigned, optimizing behavior induces an association between schooling and ability. This generates the ability bias. %

\begin{align*} E[ f(S_0 + 1, \mu) \mid \mu > \mu^*] - E[ f(S_0, \mu) \mid \mu < \mu^*] > E[ f(S_0 + 1, \mu) ] - E[ f(S_0, \mu)] \end{align*}

We now turn to the development of the Wald estimator Wald (1940). So, we first derive expected earnings equation for each age \(a\).

\begin{align*} E[\ln y_a] = \pi_1 [f(S_0 + 1, \mu_1) + g(a - a_\kappa - 1, \mu_1)] + (1 - \pi_1) [f(S_0, \mu_2) + g(a - a_\kappa, \mu_2)] \end{align*}

We now consider the following scenario, where we reduce the school entry age by one year but keep the minimum school leaving age unchanged. Type 1 achieve their optimal level of schooling exactly at the school leaving age. Type 2’s will be forced to attend school a year longer. %

\begin{align*} E[\ln y_a] = \pi_1 [f(S_0 + 1, \mu_1) + g(a - a_\kappa, \mu_1)] + (1 - \pi_1) [f(S_0 + 1, \mu_2) + g(a - a_\kappa, \mu_2)] \end{align*}

The difference in expected (ln) earnings divided by the difference in expected schooling \(0 \cdot \pi_1 + 1 \cdot (1 - \pi_1)\), the Wald estimator, is thus

\begin{align*}\begin{array}{ll} E[\ln y_a | \underbrace{Z = 1}_{\text{reduced entry age}}] - E[\ln y_a | Z = 0] \\ = \pi_1 (f(S_0 + 1, \mu_1) + g(a - a_\kappa, \mu_1)) \\ \hspace{11pt}+ (1 - \pi _1) (f(S_0 + 1, \mu_2) + g(a - o_\kappa, \mu_2)) \\ \hspace{11pt}- \pi_1 (f(S_0 + 1, \mu_1) + g(a - a_\kappa - 1, \mu_1)) \\ \hspace{11pt}- (1 - \pi_1) (f(S_0, \mu_2) + g(a - o_\kappa, \mu_2)) \\[20pt] = \pi_1 (g(a - a_\kappa, \mu_1) - g(a - a_\kappa - 1, \mu_1)) \\ \hspace{11pt}+ (1 - \pi_1) (f(S_0 + 1, \mu_2) - f(S_0, \mu_2)) \end{array}\end{align*}

divide by difference in schooling attainment

\begin{align*} \pi_1 * 0 + (1 - \pi_1) * 1 \end{align*}
\begin{align*} \frac{\Delta E (\ln y_a)}{\Delta S} = \underbrace{\frac{\pi_1}{1 -\pi_1} [g(a - a_\kappa, \mu_1) - g(a - a_\kappa - 1, \mu_1)]}_{\text{type 1's additional experience}} + \underbrace{[f(S_0 + 1, \mu_2) - f(S_0, \mu_2)]}_{\text{effect of interest (compliers only)}}, \end{align*}

where \(\frac{\Delta E (\ln y_a)}{\Delta S}\) corresponds to \(E(\ln y_a \mid Z = 1) - E(\ln y_a \mid Z = 0)\) and \(Z\) takes value one under the reduced school entry age and zero otherwise. Thus the estimate does not correspond directly to the effect of interest. However, Angrist & Krueger (1991) make the point in Figure V that for the cohort they are looking at \((a = 40, ..., 49)\) the effect of age on earnings is negligible.

Resources